What Does A Wave Carry

Repeated oscillation around equilibrium

This commodity is most waves in the scientific sense. For waves on seas and lakes, encounter Air current wave. For other uses, see Moving ridge (disambiguation).

Surface waves in water showing water ripples

In physics, mathematics, and related fields, a wave is a propagating dynamic disturbance (modify from equilibrium) of one or more quantities. Waves can be periodic, in which case those quantities oscillate repeatedly virtually an equilibrium (resting) value at some frequency. When the unabridged waveform moves in one direction, information technology is said to be a traveling moving ridge; by contrast, a pair of superimposed periodic waves traveling in opposite directions makes a standing wave. In a standing wave, the amplitude of vibration has nulls at some positions where the wave amplitude appears smaller or even aught. Waves are often described by a wave equation (standing moving ridge field of ii opposite waves) or a one-fashion wave equation for unmarried wave propagation in a defined direction.

Two types of waves are nearly commonly studied in classical physics. In a mechanical wave, stress and strain fields oscillate about a mechanical equilibrium. A mechanical wave is a local deformation (strain) in some physical medium that propagates from particle to particle by creating local stresses that cause strain in neighboring particles too. For example, sound waves are variations of the local force per unit area and particle motion that propagate through the medium. Other examples of mechanical waves are seismic waves, gravity waves, surface waves, string vibrations, and vortices. In an electromagnetic wave (such as low-cal), coupling betwixt the electrical and magnetic fields which sustains propagation of a wave involving these fields according to Maxwell's equations. Electromagnetic waves can travel through a vacuum and through some dielectric media (at wavelengths where they are considered transparent). Electromagnetic waves, according to their frequencies (or wavelengths) have more than specific designations including radio waves, infrared radiation, terahertz waves, visible lite, ultraviolet radiations, X-rays and gamma rays.

Other types of waves include gravitational waves, which are disturbances in spacetime that propagate according to general relativity; rut diffusion waves; plasma waves that combine mechanical deformations and electromagnetic fields; reaction–diffusion waves, such as in the Belousov–Zhabotinsky reaction; and many more than. Mechanical and electromagnetic waves transfer energy,^[1] momentum, and data, only they exercise not transfer particles in the medium. In mathematics and electronics waves are studied as signals.^[2] On the other hand, some waves have envelopes which do not move at all such as standing waves (which are key to music) and hydraulic jumps. Some, like the probability waves of breakthrough mechanics, may be completely static^{[ dubious – discuss ]}.

A physical wave field is almost always confined to some finite region of space, called its domain. For example, the seismic waves generated by earthquakes are meaning merely in the interior and surface of the planet, so they tin can be ignored outside it. Yet, waves with infinite domain, that extend over the whole infinite, are ordinarily studied in mathematics, and are very valuable tools for understanding concrete waves in finite domains.

A plane wave is an important mathematical idealization where the disturbance is identical along whatsoever (infinite) plane normal to a specific management of travel. Mathematically, the simplest moving ridge is a sinusoidal plane wave in which at any indicate the field experiences uncomplicated harmonic motion at 1 frequency. In linear media, complicated waves can generally be decomposed as the sum of many sinusoidal plane waves having different directions of propagation and/or different frequencies. A plane wave is classified equally a transverse moving ridge if the field disturbance at each indicate is described by a vector perpendicular to the direction of propagation (also the direction of energy transfer); or longitudinal wave if those vectors are aligned with the propagation direction. Mechanical waves include both transverse and longitudinal waves; on the other hand electromagnetic plane waves are strictly transverse while sound waves in fluids (such as air) tin can only be longitudinal. That physical management of an oscillating field relative to the propagation management is also referred to every bit the wave'due south polarization, which can be an important aspect.

Mathematical description [edit]

Unmarried waves [edit]

A wave can be described just like a field, namely equally a function ${\displaystyle F(x,t)}$ where ${\displaystyle x}$ is a position and ${\displaystyle t}$ is a time.

The value of ${\displaystyle x}$ is a point of infinite, specifically in the region where the moving ridge is divers. In mathematical terms, it is usually a vector in the Cartesian 3-dimensional space ${\displaystyle \mathbb {R} ^{3}}$ . However, in many cases one can ignore one dimension, and let ${\displaystyle x}$ be a point of the Cartesian airplane ${\displaystyle \mathbb {R} ^{2}}$ . This is the case, for example, when studying vibrations of a drum pare. One may even restrict ${\displaystyle x}$ to a bespeak of the Cartesian line ${\displaystyle \mathbb {R} }$ — that is, the set of real numbers. This is the case, for case, when studying vibrations in a violin string or recorder. The fourth dimension ${\displaystyle t}$ , on the other paw, is ever causeless to be a scalar; that is, a real number.

The value of ${\displaystyle F(10,t)}$ tin be whatever physical quantity of interest assigned to the point ${\displaystyle x}$ that may vary with time. For example, if ${\displaystyle F}$ represents the vibrations within an elastic solid, the value of ${\displaystyle F(x,t)}$ is usually a vector that gives the electric current displacement from ${\displaystyle 10}$ of the material particles that would be at the point ${\displaystyle x}$ in the absence of vibration. For an electromagnetic wave, the value of ${\displaystyle F}$ can be the electric field vector ${\displaystyle East}$ , or the magnetic field vector ${\displaystyle H}$ , or any related quantity, such as the Poynting vector ${\displaystyle E\times H}$ . In fluid dynamics, the value of ${\displaystyle F(x,t)}$ could exist the velocity vector of the fluid at the bespeak ${\displaystyle ten}$ , or whatever scalar property like pressure level, temperature, or density. In a chemic reaction, ${\displaystyle F(ten,t)}$ could be the concentration of some substance in the neighborhood of betoken ${\displaystyle 10}$ of the reaction medium.

For any dimension ${\displaystyle d}$ (ane, 2, or three), the wave'southward domain is then a subset ${\displaystyle D}$ of ${\displaystyle \mathbb {R} ^{d}}$ , such that the function value ${\displaystyle F(x,t)}$ is defined for any point ${\displaystyle ten}$ in ${\displaystyle D}$ . For instance, when describing the movement of a drum skin, one tin consider ${\displaystyle D}$ to be a disk (circle) on the plane ${\displaystyle \mathbb {R} ^{ii}}$ with center at the origin ${\displaystyle (0,0)}$ , and let ${\displaystyle F(10,t)}$ be the vertical displacement of the skin at the betoken ${\displaystyle 10}$ of ${\displaystyle D}$ and at time ${\displaystyle t}$ .

Wave families [edit]

Sometimes one is interested in a unmarried specific moving ridge. More frequently, notwithstanding, one needs to understand large set of possible waves; similar all the ways that a drum skin tin can vibrate after being struck once with a pulsate stick, or all the possible radar echos 1 could go from an airplane that may be approaching an airdrome.

In some of those situations, one may describe such a family of waves past a office ${\displaystyle F(A,B,\ldots ;x,t)}$ that depends on sure parameters ${\displaystyle A,B,\ldots }$ , likewise ${\displaystyle x}$ and ${\displaystyle t}$ . Then one can obtain different waves — that is, different functions of ${\displaystyle ten}$ and ${\displaystyle t}$ — past choosing different values for those parameters.

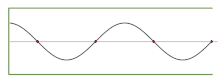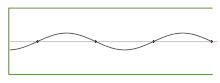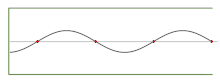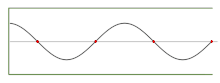
Audio pressure standing wave in a half-open pipe playing the seventh harmonic of the fundamental (n = 4)

For instance, the sound pressure inside a recorder that is playing a "pure" note is typically a continuing wave, that tin can exist written as

${\displaystyle F(A,L,n,c;x,t)=A\left(\cos 2\pi x{\frac {2n-ane}{4L}}\right)\left(\cos 2\pi ct{\frac {2n-1}{4L}}\right)}$

The parameter ${\displaystyle A}$ defines the amplitude of the moving ridge (that is, the maximum sound force per unit area in the bore, which is related to the loudness of the note); ${\displaystyle c}$ is the speed of sound; ${\displaystyle L}$ is the length of the bore; and ${\displaystyle n}$ is a positive integer (1,two,3,…) that specifies the number of nodes in the standing wave. (The position ${\displaystyle x}$ should be measured from the mouthpiece, and the time ${\displaystyle t}$ from any moment at which the pressure at the mouthpiece is maximum. The quantity ${\displaystyle \lambda =4L/(2n-1)}$ is the wavelength of the emitted note, and ${\displaystyle f=c/\lambda }$ is its frequency.) Many full general properties of these waves tin can be inferred from this full general equation, without choosing specific values for the parameters.

As another example, it may be that the vibrations of a pulsate skin after a single strike depend only on the distance ${\displaystyle r}$ from the center of the skin to the strike betoken, and on the strength ${\displaystyle s}$ of the strike. Then the vibration for all possible strikes tin be described past a part ${\displaystyle F(r,s;x,t)}$ .

Sometimes the family of waves of involvement has infinitely many parameters. For example, 1 may desire to describe what happens to the temperature in a metal bar when it is initially heated at various temperatures at different points forth its length, and and so allowed to cool by itself in vacuum. In that case, instead of a scalar or vector, the parameter would accept to be a function ${\displaystyle h}$ such that ${\displaystyle h(x)}$ is the initial temperature at each point ${\displaystyle x}$ of the bar. So the temperatures at later times tin can be expressed past a office ${\displaystyle F}$ that depends on the part ${\displaystyle h}$ (that is, a functional operator), and then that the temperature at a later on time is ${\displaystyle F(h;x,t)}$

Differential wave equations [edit]

Some other way to draw and study a family of waves is to requite a mathematical equation that, instead of explicitly giving the value of ${\displaystyle F(x,t)}$ , merely constrains how those values can change with time. Then the family unit of waves in question consists of all functions ${\displaystyle F}$ that satisfy those constraints — that is, all solutions of the equation.

This approach is extremely important in physics, because the constraints usually are a upshot of the concrete processes that cause the wave to evolve. For case, if ${\displaystyle F(x,t)}$ is the temperature inside a cake of some homogeneous and isotropic solid material, its evolution is constrained by the partial differential equation

${\displaystyle {\frac {\partial F}{\partial t}}(x,t)=\alpha \left({\frac {\partial ^{two}F}{\partial x_{1}^{ii}}}(10,t)+{\frac {\fractional ^{2}F}{\fractional x_{two}^{2}}}(10,t)+{\frac {\fractional ^{2}F}{\fractional x_{3}^{2}}}(x,t)\right)+\beta Q(x,t)}$

where ${\displaystyle Q(p,f)}$ is the heat that is being generated per unit of volume and fourth dimension in the neighborhood of ${\displaystyle x}$ at time ${\displaystyle t}$ (for instance, by chemical reactions happening there); ${\displaystyle x_{ane},x_{two},x_{three}}$ are the Cartesian coordinates of the indicate ${\displaystyle x}$ ; ${\displaystyle \partial F/\fractional t}$ is the (first) derivative of ${\displaystyle F}$ with respect to ${\displaystyle t}$ ; and ${\displaystyle \partial ^{2}F/\partial x_{i}^{2}}$ is the 2nd derivative of ${\displaystyle F}$ relative to ${\displaystyle x_{i}}$ . (The symbol " ${\displaystyle \fractional }$ " is meant to signify that, in the derivative with respect to some variable, all other variables must be considered fixed.)

This equation can be derived from the laws of physics that govern the diffusion of heat in solid media. For that reason, it is called the rut equation in mathematics, even though it applies to many other physical quantities also temperatures.

For some other case, we can describe all possible sounds echoing inside a container of gas by a function ${\displaystyle F(10,t)}$ that gives the pressure at a point ${\displaystyle x}$ and fourth dimension ${\displaystyle t}$ within that container. If the gas was initially at compatible temperature and limerick, the evolution of ${\displaystyle F}$ is constrained past the formula

${\displaystyle {\frac {\partial ^{2}F}{\partial t^{two}}}(ten,t)=\alpha \left({\frac {\partial ^{2}F}{\partial x_{1}^{two}}}(x,t)+{\frac {\partial ^{2}F}{\fractional x_{two}^{2}}}(x,t)+{\frac {\fractional ^{2}F}{\partial x_{three}^{2}}}(x,t)\right)+\beta P(x,t)}$

Hither ${\displaystyle P(x,t)}$ is some extra compression forcefulness that is existence applied to the gas near ${\displaystyle x}$ by some external procedure, such as a loudspeaker or piston right next to ${\displaystyle p}$ .

This same differential equation describes the beliefs of mechanical vibrations and electromagnetic fields in a homogeneous isotropic non-conducting solid. Note that this equation differs from that of rut menstruation only in that the left-hand side is ${\displaystyle \partial ^{2}F/\partial t^{two}}$ , the 2d derivative of ${\displaystyle F}$ with respect to fourth dimension, rather than the showtime derivative ${\displaystyle \partial F/\fractional t}$ . Notwithstanding this small change makes a huge difference on the prepare of solutions ${\displaystyle F}$ . This differential equation is called "the" wave equation in mathematics, even though it describes only one very special kind of waves.

Wave in elastic medium [edit]

Consider a traveling transverse wave (which may be a pulse) on a string (the medium). Consider the string to have a unmarried spatial dimension. Consider this wave as traveling

Wavelength λ, can be measured betwixt whatsoever two respective points on a waveform

Animation of two waves, the green wave moves to the right while blueish wave moves to the left, the cyberspace reddish wave aamplitude at each bespeak is the sum of the amplitudes of the individual waves. Note that f(x,t) + k(x,t) = u(10,t)

This wave tin then be described by the two-dimensional functions

${\displaystyle u(x,t)=F(10-vt)}$ (waveform ${\displaystyle F}$ traveling to the correct)

${\displaystyle u(x,t)=G(x+vt)}$ (waveform ${\displaystyle Yard}$ traveling to the left)

or, more mostly, past d'Alembert's formula:^[6]

${\displaystyle u(x,t)=F(x-vt)+Yard(ten+vt).}$

representing 2 component waveforms ${\displaystyle F}$ and ${\displaystyle G}$ traveling through the medium in opposite directions. A generalized representation of this wave tin be obtained^[7] as the partial differential equation

${\displaystyle {\frac {1}{five^{2}}}{\frac {\partial ^{2}u}{\fractional t^{2}}}={\frac {\partial ^{2}u}{\partial ten^{two}}}.}$

General solutions are based upon Duhamel's principle.^[viii]

Abreast the 2d club wave equations that are describing a standing wave field, the one-fashion wave equation describes the propagation of single moving ridge in a divers management.

Wave forms [edit]

The form or shape of F in d'Alembert's formula involves the argument x − vt. Constant values of this argument correspond to constant values of F, and these constant values occur if x increases at the same charge per unit that vt increases. That is, the wave shaped like the part F will move in the positive ten-direction at velocity 5 (and 1000 will propagate at the aforementioned speed in the negative ten-direction).^[9]

In the case of a periodic part F with flow λ, that is, F(x + λ − vt) = F(x − vt), the periodicity of F in infinite means that a snapshot of the wave at a given time t finds the wave varying periodically in infinite with period λ (the wavelength of the wave). In a similar fashion, this periodicity of F implies a periodicity in time besides: F(10 − v(t + T)) = F(x − vt) provided vT = λ, so an observation of the wave at a fixed location x finds the wave undulating periodically in time with period T = λ/five.^[x]

Amplitude and modulation [edit]

Amplitude modulation can be achieved through f(x,t) = 1.00×sin(2π/0.x×(x−1.00×t)) and g(x,t) = 1.00×sin(2π/0.xi×(x−1.00×t))only the resultant is visible to meliorate clarity of waveform.

Illustration of the envelope (the slowly varying red curve) of an aamplitude-modulated wave. The fast varying blue curve is the carrier wave, which is being modulated.

The amplitude of a wave may be constant (in which case the wave is a c.west. or continuous wave), or may exist modulated and so as to vary with fourth dimension and/or position. The outline of the variation in amplitude is chosen the envelope of the wave. Mathematically, the modulated moving ridge can be written in the grade:^{[11] [12] [13]}

${\displaystyle u(x,t)=A(x,t)\sin \left(kx-\omega t+\phi \right),}$

where ${\displaystyle A(x,\ t)}$ is the amplitude envelope of the wave, ${\displaystyle 1000}$ is the wavenumber and ${\displaystyle \phi }$ is the phase. If the group velocity ${\displaystyle v_{g}}$ (see below) is wavelength-independent, this equation can be simplified equally:^[xiv]

${\displaystyle u(ten,t)=A(x-v_{g}t)\sin \left(kx-\omega t+\phi \right),}$

showing that the envelope moves with the group velocity and retains its shape. Otherwise, in cases where the group velocity varies with wavelength, the pulse shape changes in a way often described using an envelope equation.^{[fourteen] [15]}

Phase velocity and group velocity [edit]

There are 2 velocities that are associated with waves, the phase velocity and the group velocity.

Stage velocity is the charge per unit at which the phase of the wave propagates in space: any given phase of the moving ridge (for example, the crest) will appear to travel at the phase velocity. The phase velocity is given in terms of the wavelength λ (lambda) and period T every bit

${\displaystyle v_{\mathrm {p} }={\frac {\lambda }{T}}.}$

A moving ridge with the group and phase velocities going in unlike directions

Group velocity is a property of waves that have a defined envelope, measuring propagation through space (that is, phase velocity) of the overall shape of the waves' amplitudes – modulation or envelope of the wave.

Special waves [edit]

Sine waves [edit]

Airplane waves [edit]

A aeroplane wave is a kind of wave whose value varies just in one spatial direction. That is, its value is constant on a plane that is perpendicular to that direction. Aeroplane waves can be specified past a vector of unit length ${\displaystyle {\hat {n}}}$ indicating the management that the wave varies in, and a wave profile describing how the wave varies as a function of the deportation along that direction ( ${\displaystyle {\hat {n}}\cdot {\vec {x}}}$ ) and time ( ${\displaystyle t}$ ). Since the moving ridge profile merely depends on the position ${\displaystyle {\vec {x}}}$ in the combination ${\displaystyle {\hat {n}}\cdot {\vec {10}}}$ , whatsoever displacement in directions perpendicular to ${\displaystyle {\lid {northward}}}$ cannot bear on the value of the field.

Plane waves are frequently used to model electromagnetic waves far from a source. For electromagnetic plane waves, the electric and magnetic fields themselves are transverse to the management of propagation, and also perpendicular to each other.

Standing waves [edit]

Continuing wave. The cherry dots represent the wave nodes

A continuing wave, also known equally a stationary moving ridge, is a wave whose envelope remains in a constant position. This phenomenon arises as a result of interference betwixt two waves traveling in contrary directions.

The sum of 2 counter-propagating waves (of equal amplitude and frequency) creates a standing wave. Standing waves commonly ascend when a boundary blocks further propagation of the moving ridge, thus causing wave reflection, and therefore introducing a counter-propagating wave. For example, when a violin string is displaced, transverse waves propagate out to where the cord is held in place at the bridge and the nut, where the waves are reflected dorsum. At the bridge and nut, the 2 opposed waves are in antiphase and abolish each other, producing a node. Halfway between 2 nodes there is an antinode, where the two counter-propagating waves raise each other maximally. There is no net propagation of energy over time.

Physical properties [edit]

Light axle exhibiting reflection, refraction, transmission and dispersion when encountering a prism

Waves showroom mutual behaviors under a number of standard situations, for instance:

Manual and media [edit]

Waves normally move in a straight line (that is, rectilinearly) through a transmission medium. Such media tin can be classified into i or more of the following categories:

• A divisional medium if information technology is finite in extent, otherwise an unbounded medium
• A linear medium if the amplitudes of different waves at whatsoever particular point in the medium tin can be added
• A uniform medium or homogeneous medium if its physical properties are unchanged at different locations in space
• An anisotropic medium if one or more than of its physical backdrop differ in one or more directions
• An isotropic medium if its concrete properties are the aforementioned in all directions

Absorption [edit]

Waves are commonly divers in media which allow about or all of a wave's energy to propagate without loss. Withal materials may be characterized as "lossy" if they remove energy from a wave, commonly converting information technology into estrus. This is termed "assimilation." A material which absorbs a wave's energy, either in manual or reflection, is characterized by a refractive index which is complex. The amount of assimilation will mostly depend on the frequency (wavelength) of the wave, which, for instance, explains why objects may appear colored.

Reflection [edit]

When a moving ridge strikes a cogitating surface, it changes direction, such that the angle made past the incident wave and line normal to the surface equals the bending made by the reflected wave and the same normal line.

Refraction [edit]

Sinusoidal traveling plane moving ridge inbound a region of lower wave velocity at an angle, illustrating the decrease in wavelength and change of direction (refraction) that results.

Refraction is the miracle of a wave irresolute its speed. Mathematically, this ways that the size of the phase velocity changes. Typically, refraction occurs when a wave passes from i medium into another. The amount by which a wave is refracted past a material is given by the refractive index of the material. The directions of incidence and refraction are related to the refractive indices of the two materials past Snell'southward law.

Diffraction [edit]

A wave exhibits diffraction when information technology encounters an obstruction that bends the wave or when information technology spreads later on emerging from an opening. Diffraction effects are more than pronounced when the size of the obstacle or opening is comparable to the wavelength of the wave.

Interference [edit]

Identical waves from ii sources undergoing interference. Observed at the bottom i sees 5 positions where the waves add in stage, but in between which they are out of phase and cancel.

When waves in a linear medium (the usual case) cross each other in a region of space, they do non actually interact with each other, but proceed on as if the other 1 weren't present. However at whatsoever bespeak in that region the field quantities describing those waves add according to the superposition principle. If the waves are of the same frequency in a fixed phase human relationship, so there volition generally be positions at which the two waves are in phase and their amplitudes add, and other positions where they are out of phase and their amplitudes (partially or fully) abolish. This is called an interference pattern.

Polarization [edit]

The miracle of polarization arises when wave motion tin occur simultaneously in two orthogonal directions. Transverse waves tin be polarized, for example. When polarization is used as a descriptor without qualification, it usually refers to the special, simple case of linear polarization. A transverse wave is linearly polarized if it oscillates in only one management or aeroplane. In the case of linear polarization, information technology is ofttimes useful to add together the relative orientation of that plane, perpendicular to the direction of travel, in which the oscillation occurs, such equally "horizontal" for instance, if the airplane of polarization is parallel to the ground. Electromagnetic waves propagating in complimentary space, for example, are transverse; they can exist polarized by the use of a polarizing filter.

Longitudinal waves, such as sound waves, do not exhibit polarization. For these waves there is only one management of oscillation, that is, along the direction of travel.

Dispersion [edit]

Schematic of light being dispersed by a prism. Click to come across blitheness.

A wave undergoes dispersion when either the phase velocity or the group velocity depends on the wave frequency. Dispersion is most easily seen past letting white low-cal pass through a prism, the result of which is to produce the spectrum of colors of the rainbow. Isaac Newton performed experiments with light and prisms, presenting his findings in the Opticks (1704) that white lite consists of several colors and that these colors cannot be decomposed any further.^[xviii]

Mechanical waves [edit]

Waves on strings [edit]

The speed of a transverse wave traveling along a vibrating string (v) is directly proportional to the square root of the tension of the string (T) over the linear mass density (μ):

${\displaystyle five={\sqrt {\frac {T}{\mu }}},}$

where the linear density μ is the mass per unit length of the cord.

Acoustic waves [edit]

Acoustic or sound waves travel at speed given by

${\displaystyle five={\sqrt {\frac {B}{\rho _{0}}}},}$

or the square root of the adiabatic bulk modulus divided by the ambient fluid density (see speed of sound).

Water waves [edit]

• Ripples on the surface of a pond are actually a combination of transverse and longitudinal waves; therefore, the points on the surface follow orbital paths.
• Sound – a mechanical moving ridge that propagates through gases, liquids, solids and plasmas;
• Inertial waves, which occur in rotating fluids and are restored by the Coriolis upshot;
• Ocean surface waves, which are perturbations that propagate through water.

Seismic waves [edit]

Seismic waves are waves of energy that travel through the World's layers, and are a result of earthquakes, volcanic eruptions, magma motility, large landslides and large man-fabricated explosions that give out low-frequency acoustic energy.

Doppler effect [edit]

The Doppler upshot (or the Doppler shift) is the modify in frequency of a wave in relation to an observer who is moving relative to the wave source.^[xix] It is named after the Austrian physicist Christian Doppler, who described the phenomenon in 1842.

Shock waves [edit]

Formation of a shock wave by a plane.

A daze wave is a blazon of propagating disturbance. When a wave moves faster than the local speed of sound in a fluid, it is a daze moving ridge. Like an ordinary wave, a daze wave carries energy and can propagate through a medium; all the same, it is characterized by an abrupt, nearly discontinuous alter in pressure, temperature and density of the medium.^[20]

Other [edit]

• Waves of traffic, that is, propagation of different densities of motor vehicles, and and then forth, which tin can be modeled as kinematic waves^[21]
• Metachronal wave refers to the appearance of a traveling moving ridge produced past coordinated sequential actions.

Electromagnetic waves [edit]

An electromagnetic wave consists of ii waves that are oscillations of the electric and magnetic fields. An electromagnetic wave travels in a direction that is at right angles to the oscillation direction of both fields. In the 19th century, James Clerk Maxwell showed that, in vacuum, the electric and magnetic fields satisfy the moving ridge equation both with speed equal to that of the speed of light. From this emerged the idea that light is an electromagnetic wave. Electromagnetic waves tin can have different frequencies (and thus wavelengths), giving rise to various types of radiations such as radio waves, microwaves, infrared, visible light, ultraviolet, X-rays, and Gamma rays.

Breakthrough mechanical waves [edit]

Schrödinger equation [edit]

The Schrödinger equation describes the wave-similar behavior of particles in quantum mechanics. Solutions of this equation are wave functions which can exist used to describe the probability density of a particle.

Dirac equation [edit]

The Dirac equation is a relativistic moving ridge equation detailing electromagnetic interactions. Dirac waves accounted for the fine details of the hydrogen spectrum in a completely rigorous fashion. The wave equation also implied the being of a new form of matter, antimatter, previously unsuspected and unobserved and which was experimentally confirmed. In the context of quantum field theory, the Dirac equation is reinterpreted to draw quantum fields corresponding to spin-½ particles.

A propagating wave packet; in general, the envelope of the wave bundle moves at a different speed than the constituent waves.^[22]

de Broglie waves [edit]

Louis de Broglie postulated that all particles with momentum accept a wavelength

${\displaystyle \lambda ={\frac {h}{p}},}$

where h is Planck'southward constant, and p is the magnitude of the momentum of the particle. This hypothesis was at the ground of quantum mechanics. Nowadays, this wavelength is called the de Broglie wavelength. For instance, the electrons in a CRT display take a de Broglie wavelength of nearly 10⁻¹³ m.

A moving ridge representing such a particle traveling in the 1000-direction is expressed by the moving ridge function as follows:

${\displaystyle \psi (\mathbf {r} ,\,t=0)=Ae^{i\mathbf {chiliad\cdot r} },}$

where the wavelength is determined by the wave vector k every bit:

${\displaystyle \lambda ={\frac {2\pi }{k}},}$

and the momentum by:

${\displaystyle \mathbf {p} =\hbar \mathbf {k} .}$

Nonetheless, a moving ridge similar this with definite wavelength is not localized in infinite, and so cannot stand for a particle localized in space. To localize a particle, de Broglie proposed a superposition of different wavelengths ranging around a central value in a wave packet,^[23] a waveform often used in breakthrough mechanics to describe the moving ridge function of a particle. In a wave packet, the wavelength of the particle is not precise, and the local wavelength deviates on either side of the main wavelength value.

In representing the wave function of a localized particle, the wave packet is ofttimes taken to have a Gaussian shape and is called a Gaussian wave packet.^[24] Gaussian wave packets also are used to analyze water waves.^[25]

For example, a Gaussian wavefunction ψ might take the form:^[26]

${\displaystyle \psi (x,\,t=0)=A\exp \left(-{\frac {10^{2}}{two\sigma ^{two}}}+ik_{0}x\right),}$

at some initial time t = 0, where the fundamental wavelength is related to the central wave vector thousand ₀ as λ₀ = 2π / 1000 ₀. It is well known from the theory of Fourier analysis,^[27] or from the Heisenberg doubt principle (in the instance of breakthrough mechanics) that a narrow range of wavelengths is necessary to produce a localized moving ridge packet, and the more than localized the envelope, the larger the spread in required wavelengths. The Fourier transform of a Gaussian is itself a Gaussian.^[28] Given the Gaussian:

${\displaystyle f(ten)=e^{-x^{2}/\left(2\sigma ^{2}\correct)},}$

the Fourier transform is:

${\displaystyle {\tilde {f}}(g)=\sigma e^{-\sigma ^{2}thou^{2}/2}.}$

The Gaussian in space therefore is made up of waves:

${\displaystyle f(10)={\frac {1}{\sqrt {2\pi }}}\int _{-\infty }^{\infty }\ {\tilde {f}}(yard)e^{ikx}\ dk;}$

that is, a number of waves of wavelengths λ such that kλ = 2 π.

The parameter σ decides the spatial spread of the Gaussian along the x-axis, while the Fourier transform shows a spread in wave vector k determined past 1/σ. That is, the smaller the extent in infinite, the larger the extent in k, and hence in λ = 2π/k.

Blitheness showing the effect of a cross-polarized gravitational wave on a ring of test particles

Gravity waves [edit]

Gravity waves are waves generated in a fluid medium or at the interface between two media when the force of gravity or buoyancy tries to restore equilibrium. A ripple on a pond is one instance.

Gravitational waves [edit]

Gravitational waves too travel through space. The first ascertainment of gravitational waves was announced on 11 February 2016.^[29] Gravitational waves are disturbances in the curvature of spacetime, predicted by Einstein's theory of general relativity.

Encounter also [edit]

• Index of wave articles

Waves in general [edit]

• Wave equation, general
• 1-mode wave equation, for waves running in pre-defined direction
• Wave propagation, whatever of the means in which waves travel
• Interference (wave propagation), a miracle in which two waves superpose to form a resultant wave
• Mechanical wave, in media transmission
• Wave Motion (journal), a scientific journal
• Wavefront, an advancing surface of wave propagation

Parameters [edit]

• Phase (waves), outset or angle of a sinusoidal wave part at its origin
• Standing wave ratio, in telecommunications
• Wavelength
• Wavenumber
• Moving ridge menstruation

Waveforms [edit]

• Creeping wave, a wave diffracted effectually a sphere
• Evanescent wave
• Longitudinal moving ridge
• Periodic travelling wave
• Sine moving ridge
• Square moving ridge
• Standing wave
• Transverse wave

Electromagnetic waves [edit]

• Dyakonov surface waves
• Dyakonov–Voigt wave
• Earth-Ionosphere waveguide, in radio transmission
• Electromagnetic wave
• Electromagnetic wave equation, describes electromagnetic wave propagation
• Microwave, a form of electromagnetic radiation

In fluids [edit]

• Airy moving ridge theory, in fluid dynamics
• Capillary wave, in fluid dynamics
• Cnoidal wave, in fluid dynamics
• Edge wave, a surface gravity moving ridge fixed past refraction against a rigid purlieus
• Faraday wave, a blazon of wave in liquids
• Gravity wave, in fluid dynamics
• Sound moving ridge, a moving ridge of sound through a medium such as air or water
• Bounding main moving ridge spectrum
• Daze wave, in aerodynamics
• Internal wave, a moving ridge inside a fluid medium
• Tidal wave, a scientifically incorrect name for a tsunami
• Tollmien–Schlichting moving ridge, in fluid dynamics

In breakthrough mechanics [edit]

• Bloch'due south theorem
• Matter wave
• Airplane pilot moving ridge, in Bohmian mechanics
• Wave office
• Wave parcel
• Wave–particle duality

In relativity [edit]

• Gravitational wave, in relativity theory
• Relativistic wave equations, wave equations that consider special relativity
• pp-wave spacetime, a set of exact solutions to Einstein's field equation

Other specific types of waves [edit]

• Alfvén wave, in plasma physics
• Atmospheric moving ridge, a periodic disturbance in the fields of atmospheric variables
• Fir wave, a forest configuration
• Lamb waves, in solid materials
• Rayleigh waves, surface audio-visual waves that travel on solids
• Spin wave, in magnetism
• Spin-density wave, in solid materials
• Trojan wave packet, in particle science
• Waves in plasmas, in plasma physics

[edit]

• Shell (acoustics)
• Cymatics
• Doppler effect
• Envelope detector
• Fourier transform for computing periodicity in evenly spaced data
• Group velocity
• Harmonic
• Index of moving ridge articles
• Inertial wave
• Least-squares spectral assay for computing periodicity in unevenly spaced data
• List of waves named after people
• Phase velocity
• Reaction–diffusion system
• Resonance
• Ripple tank
• Rogue moving ridge
• Shallow water equations
• Shive wave motorcar
• Sound
• Standing wave
• Transmission medium
• Wave turbulence
• Wind moving ridge

References [edit]

1. ^ (Hall 1982, p. viii) harv mistake: no target: CITEREFHall1982 (assist)
2. ^ Pragnan Chakravorty, "What Is a Signal? [Lecture Notes]," IEEE Signal Processing Magazine, vol. 35, no. 5, pp. 175-177, Sept. 2018. doi:10.1109/MSP.2018.2832195
3. ^ Santos, Edgar; Schöll, Michael; Sánchez-Porras, Renán; Dahlem, Markus A.; Silos, Humberto; Unterberg, Andreas; Dickhaus, Hartmut; Sakowitz, Oliver W. (2014-10-01). "Radial, spiral and reverberating waves of spreading depolarization occur in the gyrencephalic brain". NeuroImage. 99: 244–255. doi:10.1016/j.neuroimage.2014.05.021. ISSN 1095-9572. PMID 24852458. S2CID 1347927.
4. ^ Michael A. Slawinski (2003). "Wave equations". Seismic waves and rays in elastic media. Elsevier. pp. 131 ff. ISBN978-0-08-043930-3.
5. ^ Lev A. Ostrovsky & Alexander I. Potapov (2001). Modulated waves: theory and application. Johns Hopkins University Printing. ISBN978-0-8018-7325-6.
6. ^ Karl F Graaf (1991). Wave motility in elastic solids (Reprint of Oxford 1975 ed.). Dover. pp. xiii–14. ISBN978-0-486-66745-iv.
7. ^ For an example derivation, run across the steps leading upwards to eq. (17) in Francis Redfern. "Kinematic Derivation of the Moving ridge Equation". Physics Periodical. Archived from the original on 2013-07-24. Retrieved 2012-12-11 .
8. ^ Jalal M. Ihsan Shatah; Michael Struwe (2000). "The linear wave equation". Geometric wave equations. American Mathematical Society Bookstore. pp. 37ff. ISBN978-0-8218-2749-9.
9. ^ Louis Lyons (1998). All you wanted to know about mathematics merely were afraid to ask. Cambridge University Press. pp. 128 ff. ISBN978-0-521-43601-4.
10. ^ Alexander McPherson (2009). "Waves and their properties". Introduction to Macromolecular Crystallography (2 ed.). Wiley. p. 77. ISBN978-0-470-18590-two.
11. ^ Christian Jirauschek (2005). FEW-cycle Laser Dynamics and Carrier-envelope Phase Detection. Cuvillier Verlag. p. 9. ISBN978-3-86537-419-half dozen.
12. ^ Fritz Kurt Kneubühl (1997). Oscillations and waves. Springer. p. 365. ISBN978-3-540-62001-3.
13. ^ Mark Lundstrom (2000). Fundamentals of carrier transport. Cambridge University Printing. p. 33. ISBN978-0-521-63134-1.
14. ^ ^{a b} Mentum-Lin Chen (2006). "§13.7.three Pulse envelope in nondispersive media". Foundations for guided-wave optics. Wiley. p. 363. ISBN978-0-471-75687-3.
15. ^ Stefano Longhi; Davide Janner (2008). "Localization and Wannier wave packets in photonic crystals". In Hugo East. Hernández-Figueroa; Michel Zamboni-Rached; Erasmo Recami (eds.). Localized Waves. Wiley-Interscience. p. 329. ISBN978-0-470-10885-7.
16. ^ "Sine Wave". Mathematical Mysteries. 2021-11-17. Retrieved 2022-09-30 .
17. ^ "Sinusoidal". world wide web.math.cyberspace . Retrieved 2022-09-thirty .
18. ^ Newton, Isaac (1704). "Prop Seven Theor V". Opticks: Or, A treatise of the Reflections, Refractions, Inflexions and Colours of Low-cal. Also Two treatises of the Species and Magnitude of Curvilinear Figures. Vol. one. London. p. 118. All the Colours in the Universe which are fabricated by Light... are either the Colours of homogeneal Lights, or compounded of these...
19. ^ Giordano, Nicholas (2009). College Physics: Reasoning and Relationships. Cengage Learning. pp. 421–424. ISBN978-0534424718.
20. ^ Anderson, John D. Jr. (January 2001) [1984], Fundamentals of Aerodynamics (tertiary ed.), McGraw-Colina Science/Applied science/Math, ISBN978-0-07-237335-6
21. ^ Chiliad.J. Lighthill; Yard.B. Whitham (1955). "On kinematic waves. 2. A theory of traffic flow on long crowded roads". Proceedings of the Majestic Social club of London. Series A. 229 (1178): 281–345. Bibcode:1955RSPSA.229..281L. CiteSeerX10.ane.1.205.4573. doi:10.1098/rspa.1955.0088. S2CID 18301080. And: P.I. Richards (1956). "Shockwaves on the highway". Operations Research. four (one): 42–51. doi:10.1287/opre.4.1.42.
22. ^ A.T. Fromhold (1991). "Wave packet solutions". Quantum Mechanics for Applied Physics and Engineering science (Reprint of Academic Press 1981 ed.). Courier Dover Publications. pp. 59 ff. ISBN978-0-486-66741-6. (p. 61) ...the individual waves move more slowly than the packet and therefore pass back through the bundle as it advances
23. ^ Ming Chiang Li (1980). "Electron Interference". In Fifty. Marton; Claire Marton (eds.). Advances in Electronics and Electron Physics. Vol. 53. Academic Press. p. 271. ISBN978-0-12-014653-6.
24. ^ Meet for example Walter Greiner; D. Allan Bromley (2007). Quantum Mechanics (2 ed.). Springer. p. 60. ISBN978-three-540-67458-0. and John Joseph Gilman (2003). Electronic basis of the strength of materials. Cambridge University Press. p. 57. ISBN978-0-521-62005-five. ,Donald D. Fitts (1999). Principles of quantum mechanics. Cambridge University Printing. p. 17. ISBN978-0-521-65841-half dozen. .
25. ^ Chiang C. Mei (1989). The applied dynamics of ocean surface waves (2nd ed.). Earth Scientific. p. 47. ISBN978-9971-five-0789-3.
26. ^ Walter Greiner; D. Allan Bromley (2007). Quantum Mechanics (2nd ed.). Springer. p. threescore. ISBN978-three-540-67458-0.
27. ^ Siegmund Brandt; Hans Dieter Dahmen (2001). The moving picture book of breakthrough mechanics (tertiary ed.). Springer. p. 23. ISBN978-0-387-95141-vi.
28. ^ Cyrus D. Cantrell (2000). Modern mathematical methods for physicists and engineers . Cambridge University Press. p. 677. ISBN978-0-521-59827-9.
29. ^ "Gravitational waves detected for 1st time, 'opens a brand new window on the universe'". Canadian Dissemination Corporation. 11 February 2016.

Sources [edit]

• Fleisch, D.; Kinnaman, L. (2015). A student'due south guide to waves. Cambridge: Cambridge Academy Printing. Bibcode:2015sgw..volume.....F. ISBN978-1107643260.
• Campbell, Murray; Greated, Clive (2001). The musician's guide to acoustics (Repr. ed.). Oxford: Oxford University Press. ISBN978-0198165057.
• French, A.P. (1971). Vibrations and Waves (Grand.I.T. Introductory physics series). Nelson Thornes. ISBN978-0-393-09936-2. OCLC 163810889.
• Hall, D.E. (1980). Musical Acoustics: An Introduction. Belmont, CA: Wadsworth Publishing Company. ISBN978-0-534-00758-four. .
• Hunt, Frederick Vinton (1978). Origins in acoustics. Woodbury, NY: Published for the Acoustical Club of America through the American Institute of Physics. ISBN978-0300022209.
• Ostrovsky, L.A.; Potapov, A.S. (1999). Modulated Waves, Theory and Applications. Baltimore: The Johns Hopkins University Printing. ISBN978-0-8018-5870-3. .
• Griffiths, G.; Schiesser, W.Eastward. (2010). Traveling Wave Analysis of Partial Differential Equations: Numerical and Analytical Methods with Matlab and Maple. Academic Press. ISBN9780123846532.

External links [edit]

• The Feynman Lectures on Physics: Waves
• Interactive Visual Representation of Waves
• Linear and nonlinear waves
• Science Aid: Wave backdrop – Curtailed guide aimed at teens

What Does A Wave Carry,

Source: https://en.wikipedia.org/wiki/Wave

Posted by: gardnerdahme1991.blogspot.com

Share this post